Selected research topics
Metamaterials
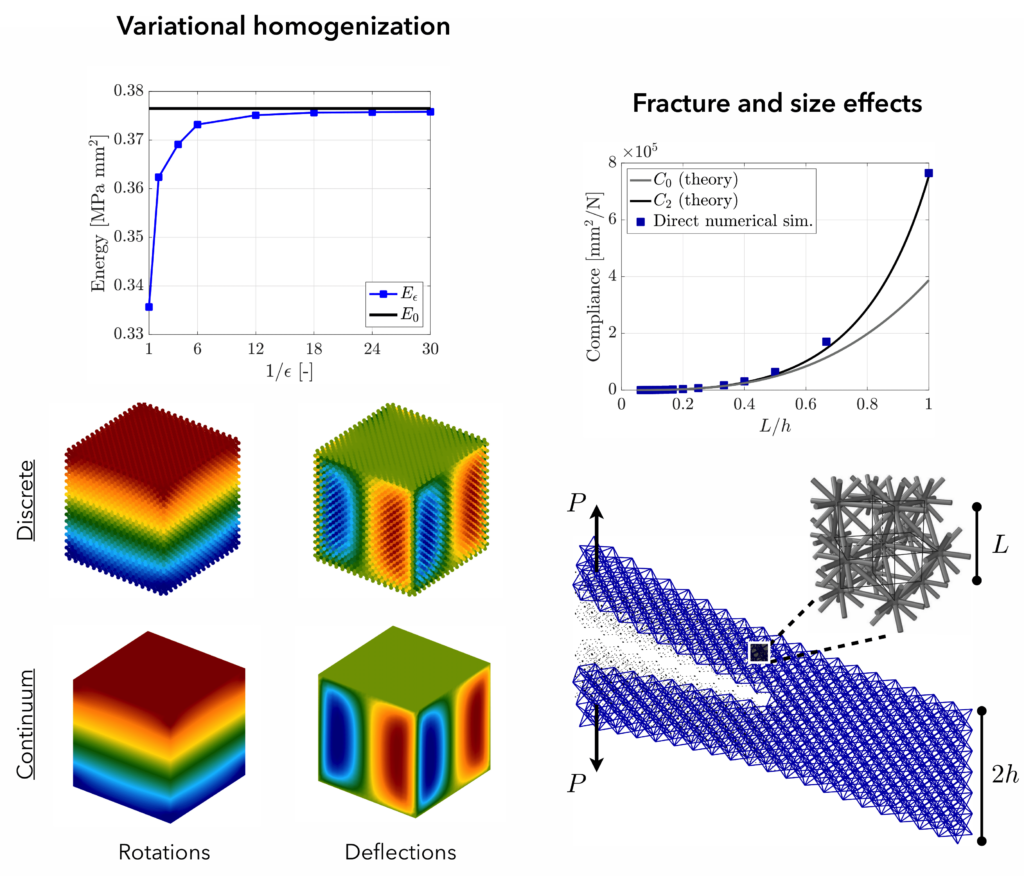
Metamaterials, or architected materials, exhibit exceptional properties and enable efficient, lightweight material use. Direct numerical simulations of these materials are prohibitively expensive due to the scale separation between the lattice and the macrostructure. Consequently, our work focuses on developing and implementing homogenized models derived rigorously from variational methods. These models, suitable for finite element implementation, provide ansatz-free and parameter-free representations of mechanical metamaterials at the continuum scale and showcase remarkable properties.
Relevant topics include:
- Generalized elasticity;
- Fracture and size effects;
- Discrete-to-continuum methods;
- Homogenization;
- Calculus of variations;
- Material design.
Outlook: non-linear behavior, multi-physics coupling, non-local behavior, etc.
Data-driven computing
Phenomenological constitutive models are valuable for describing materials at the continuum scale but are inherently empirical, often leading to epistemic uncertainty and limited predictive ability. In the spirit of parameter-free continuum modeling, our work on data-driven computing focuses on developing computational tools for multi-scale analysis that address these limitations, enforcing the fundamental laws of continuum mechanics while extracting material behavior directly from empirical data, either from experiments or lower-scale simulations. This framework provides unique opportunities in computational mechanics and fosters unprecedented synergies with data science and other emerging research areas.
Topics of interest include:
- Non-linear material behavior;
- Diffusion problems;
- Multi-scale analysis;
- Material failure;
- Data acquisition;
- Data mining;
- Data-driven methods and AI.
Outlook: data acquisition, data-driven identification, fracture, applications to energy systems, applications to biomechanics, granular media, etc.
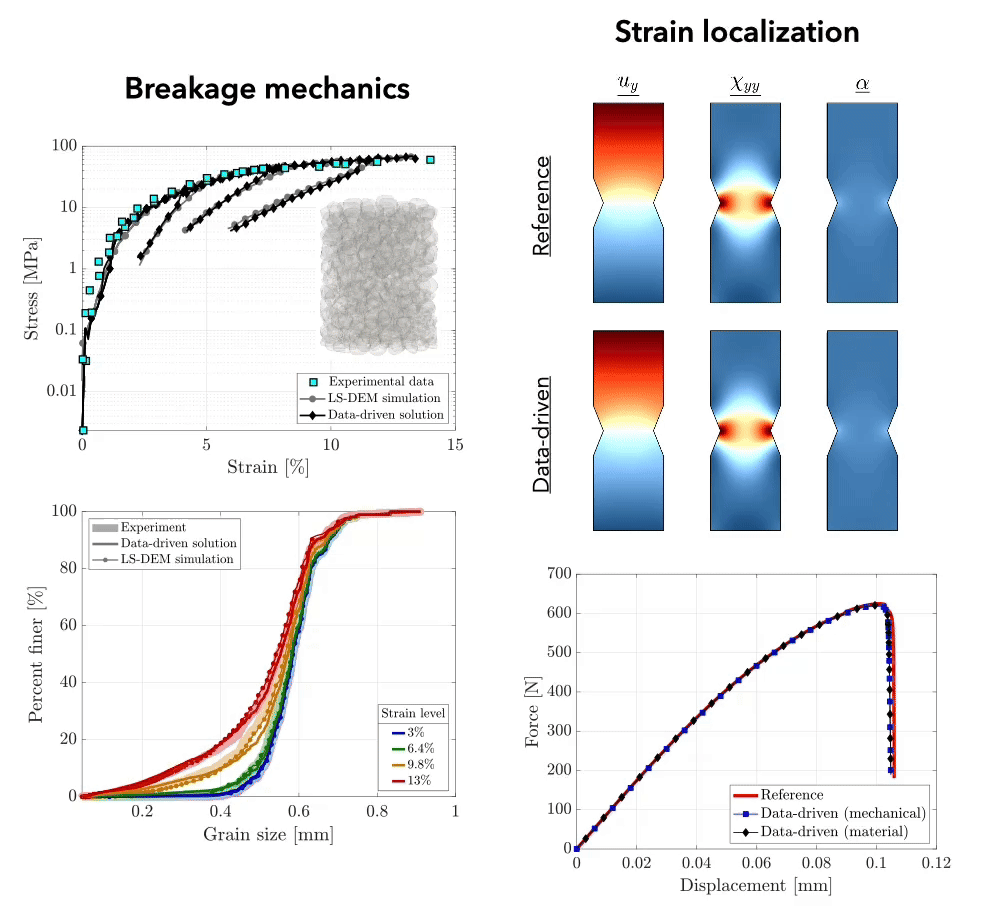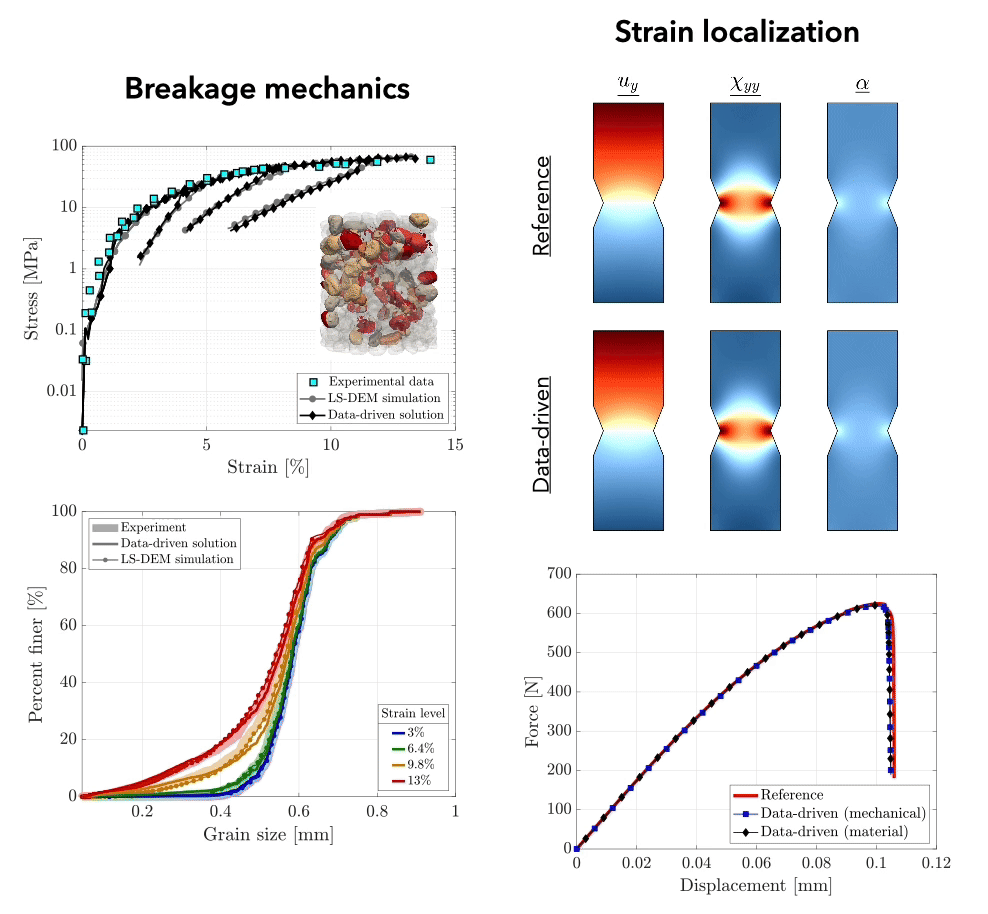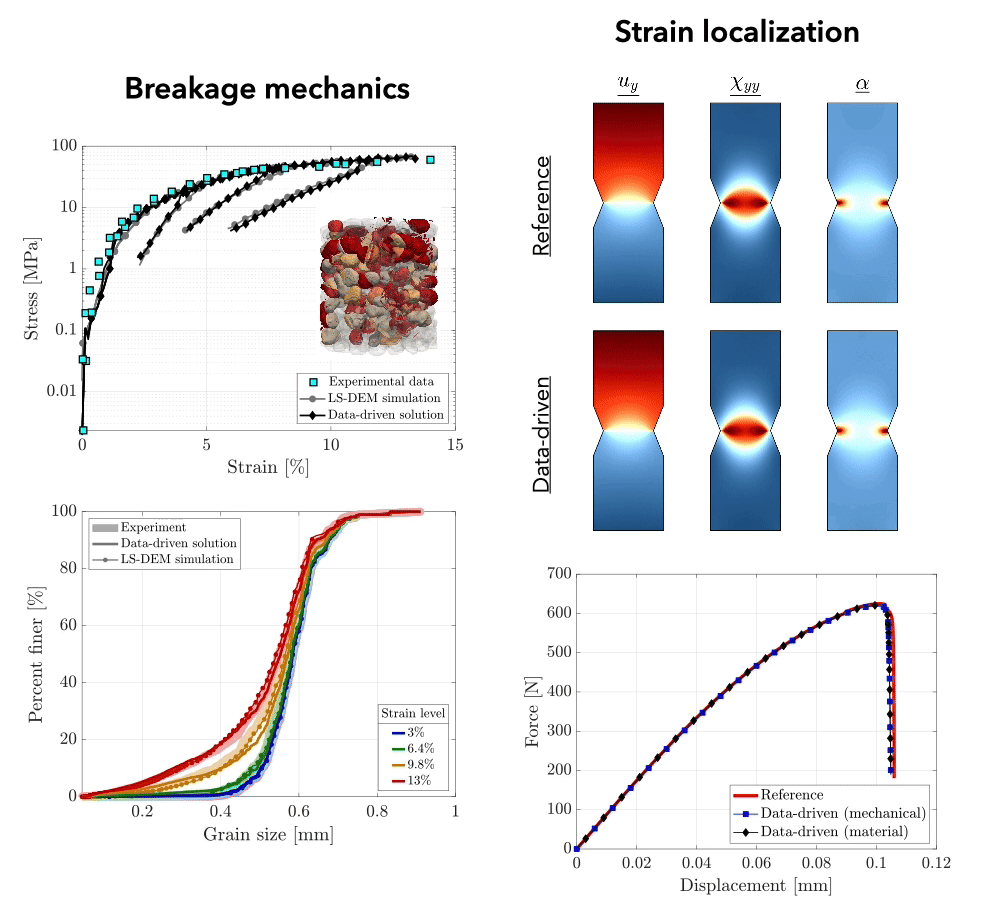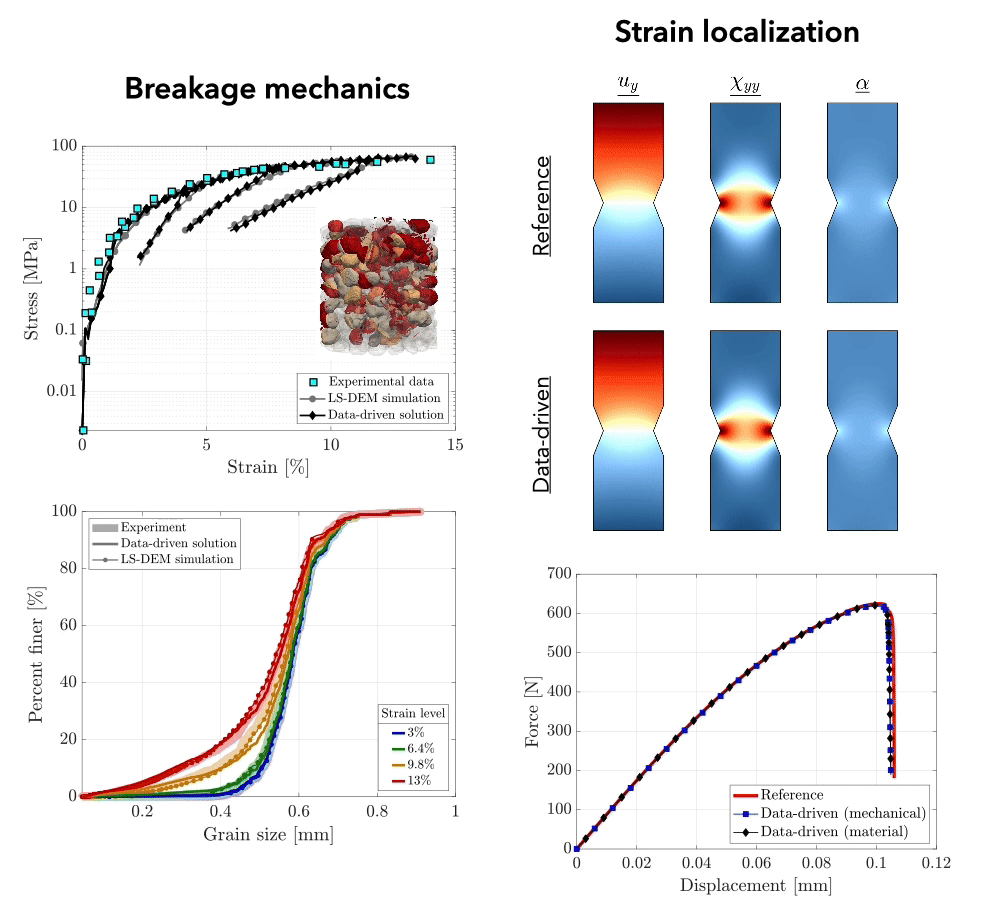
Particulate materials
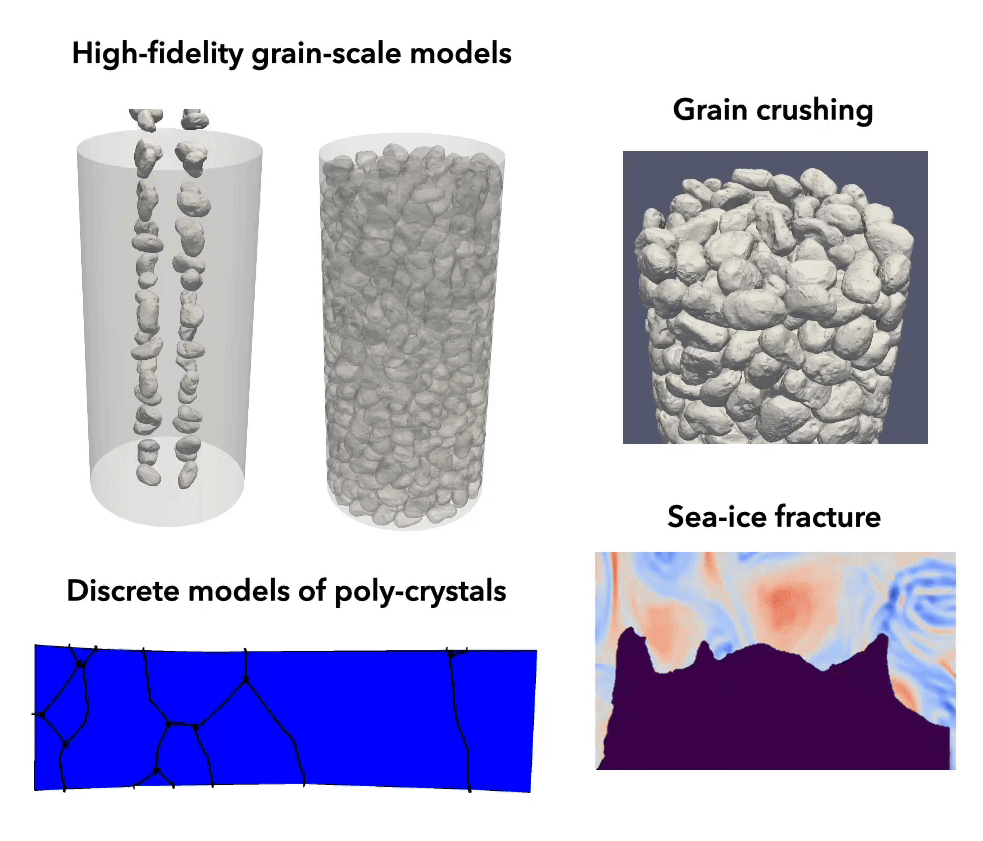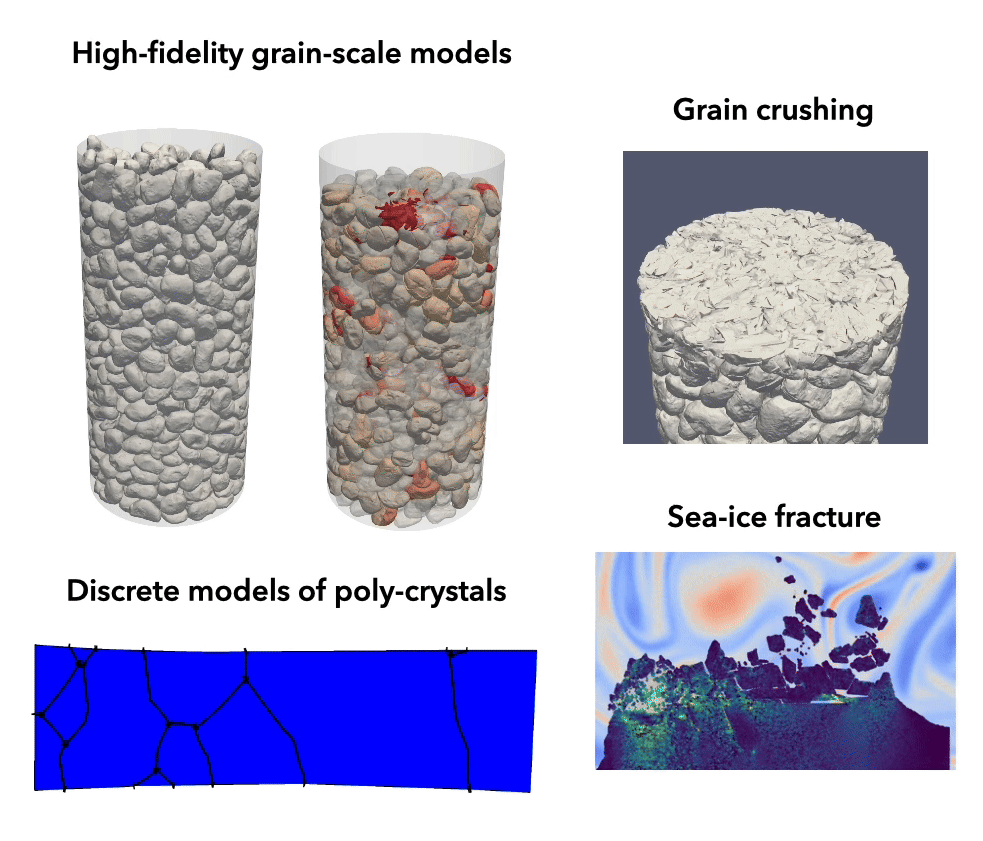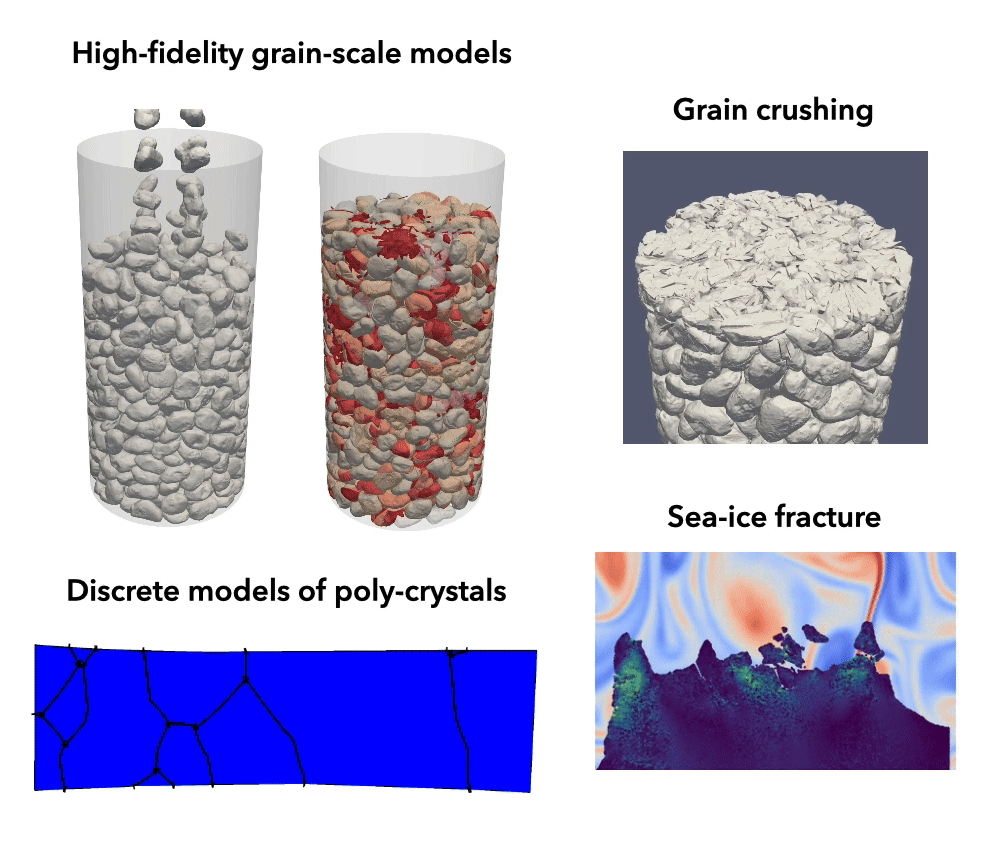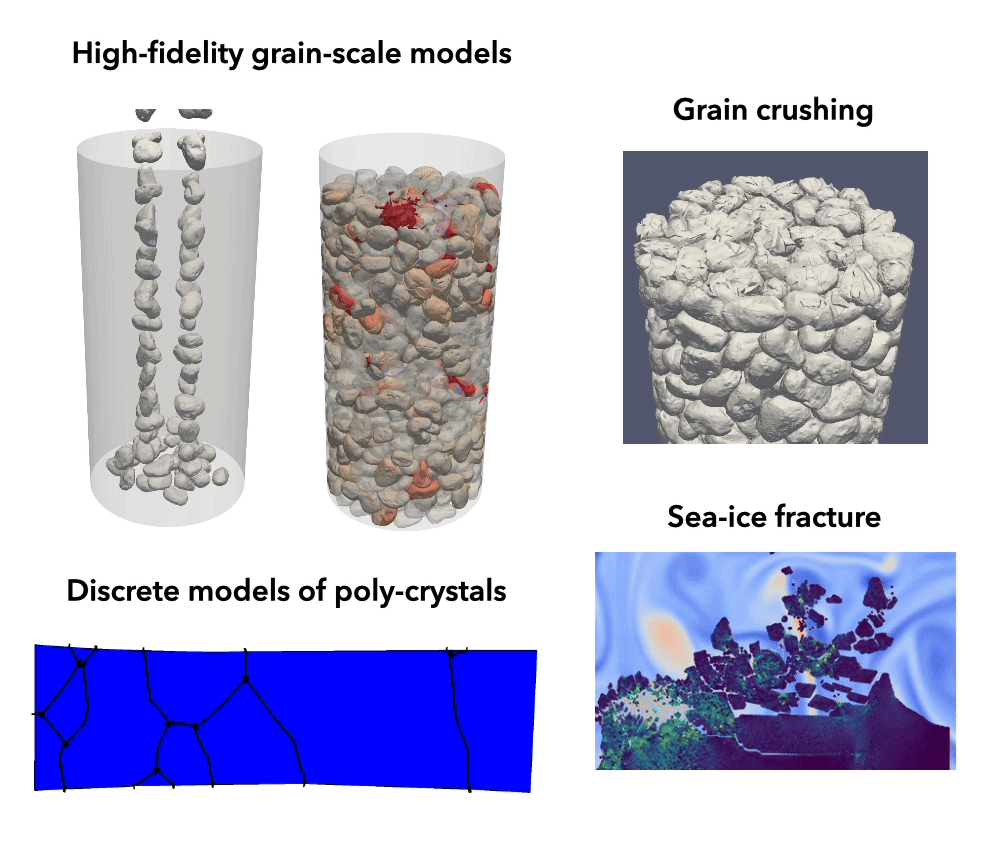
In contrast to continuum models, micromechanical models provide a detailed grain-scale description of the micromechanics underpinning the emergent behavior of particulate materials. Traditional approaches, such as conventional discrete element methods, rely on simplified particle shapes, limiting their predictive ability. In contrast, modern methods, such as the level-set discrete element method, enable high-fidelity simulations based on grain-to-grain digital twins of real particles, offering unprecedented predictive accuracy. Our group leverages and extends these advanced computational technologies to enhance our understanding of the mechanics and physics of particulate materials across a wide range of scales and applications.
Topics of interest include:
- Granular media;
- Geomechanics;
- Disordered media;
- Metamaterials;
- Digital twins;
- Material processing;
- Breakage and comminution;
- Homogenization.
Outlook: multi-physics coupling at the grain scale, applications to energy systems (e.g., modeling batteries), crystalline materials; etc.
Constitutive modeling
Constitutive models remain the standard approach for describing material behavior at the scale of engineering applications. Recognizing their importance, our research focuses on developing predictive, state-of-the-art constitutive models that capture complex behaviors across a wide range of materials. Our emphasis lies in ensuring thermodynamic and variational consistency, providing robust formulations that respect the fundamental principles of mechanics. By integrating these principles with advanced computational techniques, we aim to enhance the accuracy and reliability of simulations, enabling their application to challenging problems in engineering and materials science.
Topics of interest include:
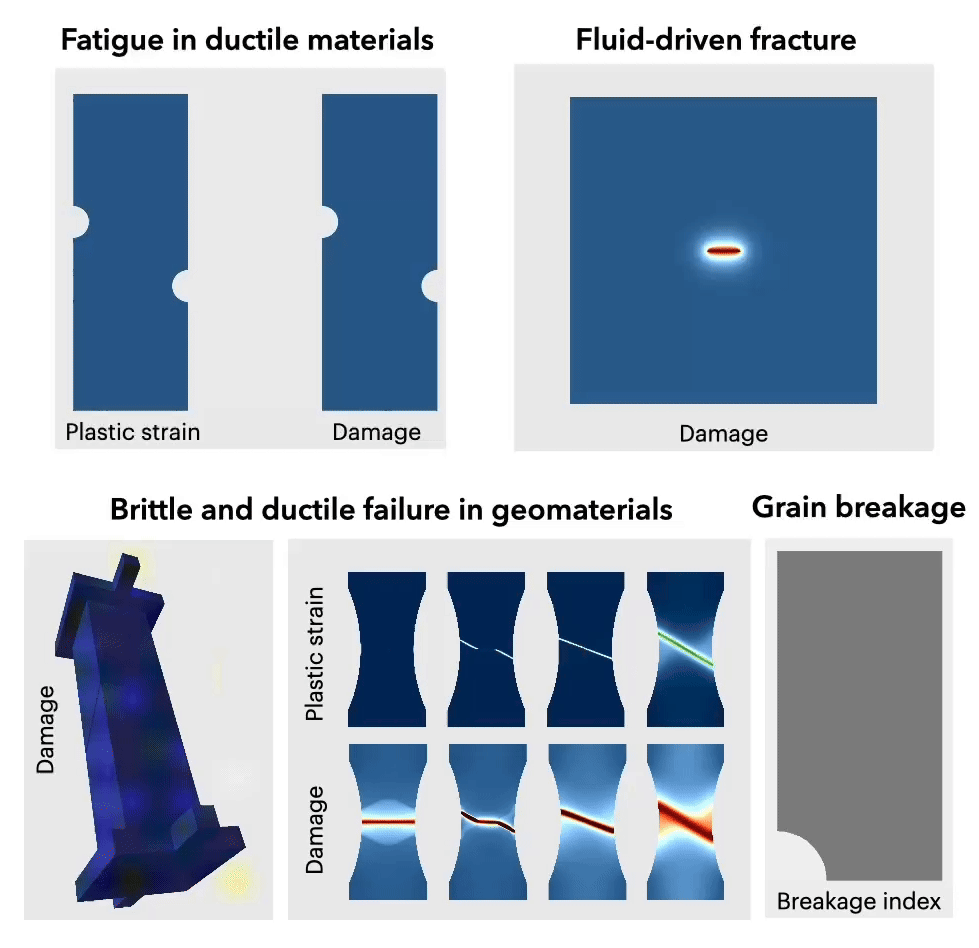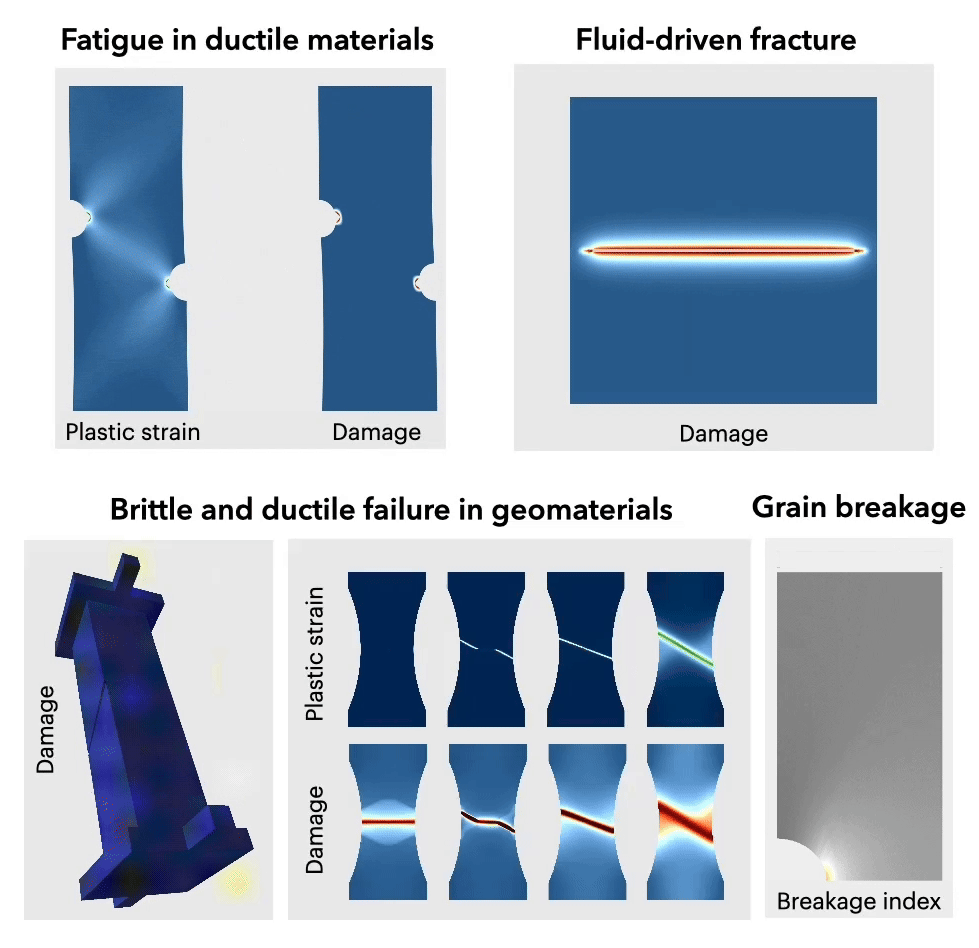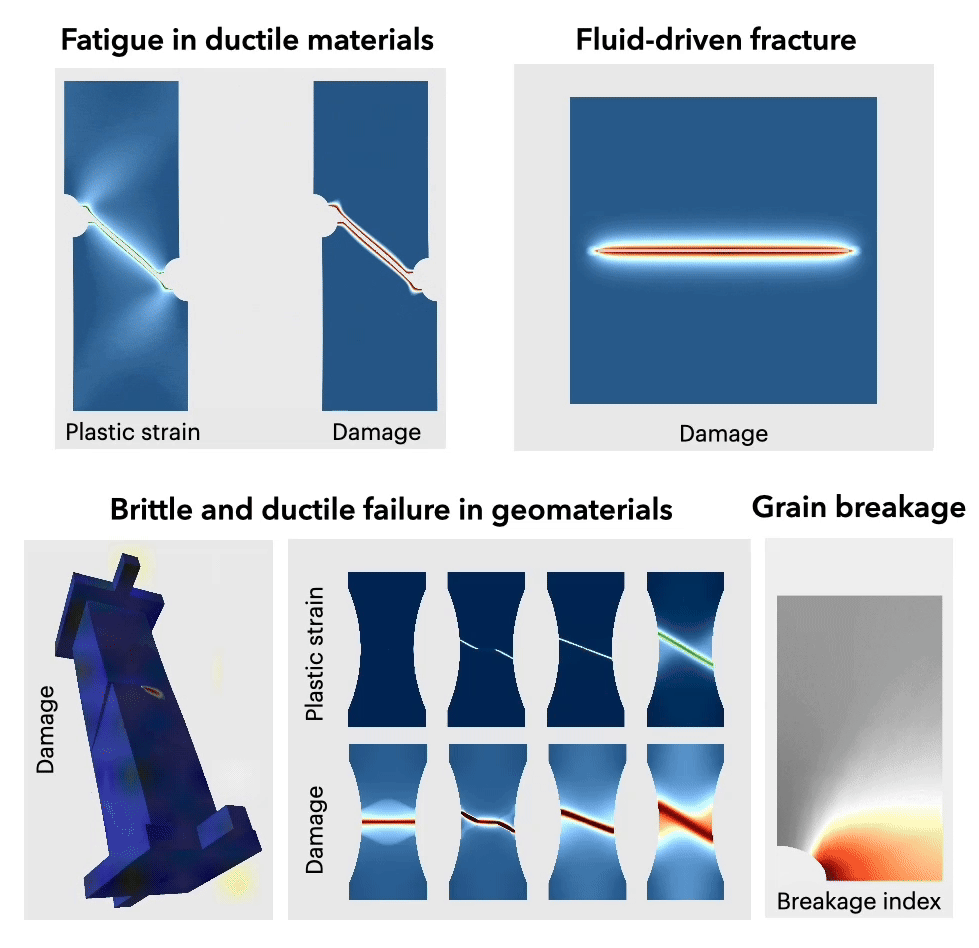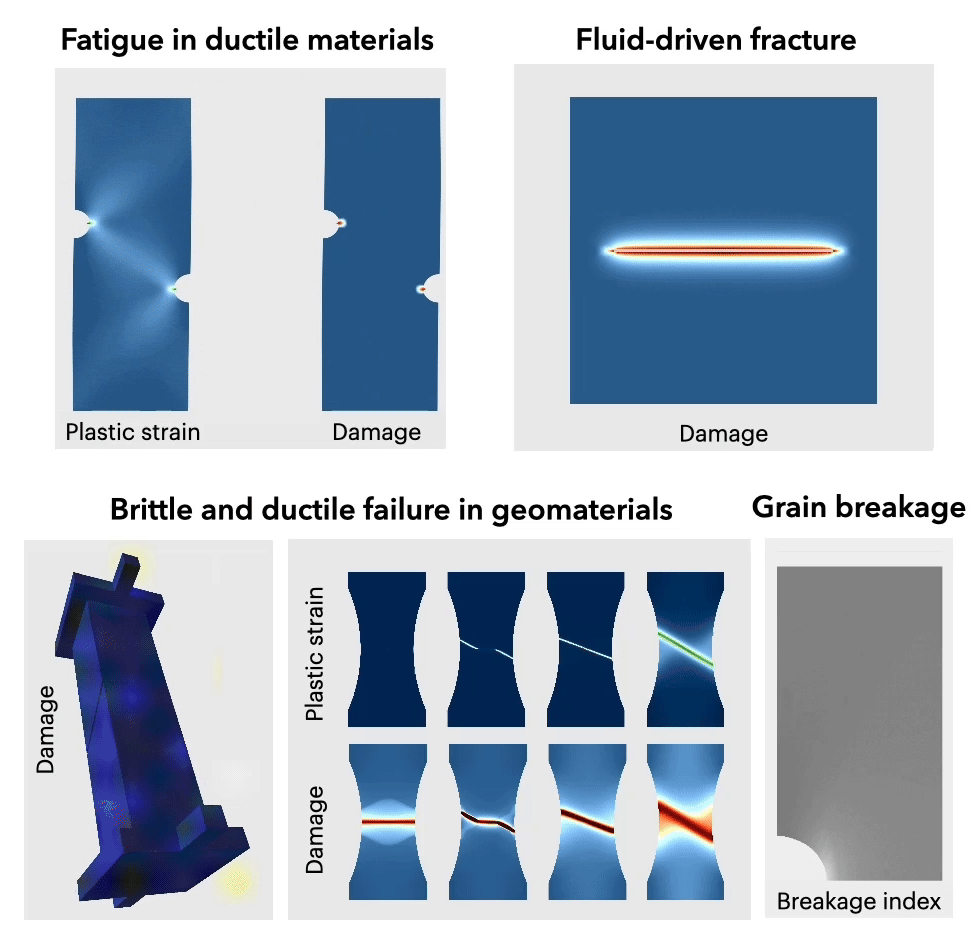
- Plasticity;
- Damage/phase-field modeling of fracture;
- Fatigue;
- Geomaterials;
- Mechanistic models;
- Micromechanics;
- Multi-physics systems.
Outlook: next generation of micromechanics/physics-based constitutive models, multi-physics models, energy applications, etc.